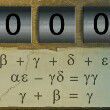怎么解这个方程? 80
3个回答
展开全部
这个方程无解
或者说有无数个解
一般解法:
1.去分母:在方程两边都乘以各分母的最小公倍数(不含分母的项也要乘);
2.去括号:先去小括号,再去中括号,最后去大括号;(记住如括号外有减号的话一定要变号)
3.移项:把含有未知数的项都移到方程的一边,其他项都移到方程的另一边;移项要变号
4.合并同类项:把方程化成ax=b(a≠0)的形式;
5.系数为成1:在方程两边都除以未知数的系数a,得到方程的解x=b/a.
同解方程
如果两个方程的解相同,那么这两个方程叫做同解方程.
方程的同解原理:
⒈方程的两边都加或减同一个数或同一个等式所得的方程与原方程是同解方程.
⒉方程的两边同乘或同除同一个不为0的数所得的方程与原方程是同解方程.
做一元一次方程应用题的重要方法:
⒈认真审题(审题)
⒉分析已知和未知量
⒊找一个合适的等量关系
⒋设一个恰当的未知数
⒌列出合理的方程 (列式)
⒍解出方程(解题)
⒎检验
⒏写出答案(作答)
ax=b
当a≠0,b=0时,
ax=0
x=0
当a≠0时,x=b/a.
当a=0,b=0时,方程有无数个解(注意:这种情况不属于一元一次方程,而属于恒等方程)
当a=0,b≠0时,方程无解
例:
(3x+1)/2-2=(3x-2)/10-(2x+3)/5
去分母(方程两边同乘各分母的最小公倍数)得,
↓
5(3x+1)-10×2=(3x-2)-2(2x+3)
去括号得,
↓
15x+5-20=3x-2-4x-6
移项得,
↓
15x-3x+4x=-2-6-5+20
合并同类项得,
↓
16x=7
系数化为1得,
↓
x=7/16.
字母公式
a=b a+c=b+c a-c=b-c
a=b ac=bc
a=bc(c≠0)= a÷c=b÷c
求根公式
由于一元一次方程是基本方程,故教科书上的解法只有上述的方法.
但对于标准形式下的一元一次方程 aX+b=0
可得出求根公式 X= -(b/a)
或者说有无数个解
一般解法:
1.去分母:在方程两边都乘以各分母的最小公倍数(不含分母的项也要乘);
2.去括号:先去小括号,再去中括号,最后去大括号;(记住如括号外有减号的话一定要变号)
3.移项:把含有未知数的项都移到方程的一边,其他项都移到方程的另一边;移项要变号
4.合并同类项:把方程化成ax=b(a≠0)的形式;
5.系数为成1:在方程两边都除以未知数的系数a,得到方程的解x=b/a.
同解方程
如果两个方程的解相同,那么这两个方程叫做同解方程.
方程的同解原理:
⒈方程的两边都加或减同一个数或同一个等式所得的方程与原方程是同解方程.
⒉方程的两边同乘或同除同一个不为0的数所得的方程与原方程是同解方程.
做一元一次方程应用题的重要方法:
⒈认真审题(审题)
⒉分析已知和未知量
⒊找一个合适的等量关系
⒋设一个恰当的未知数
⒌列出合理的方程 (列式)
⒍解出方程(解题)
⒎检验
⒏写出答案(作答)
ax=b
当a≠0,b=0时,
ax=0
x=0
当a≠0时,x=b/a.
当a=0,b=0时,方程有无数个解(注意:这种情况不属于一元一次方程,而属于恒等方程)
当a=0,b≠0时,方程无解
例:
(3x+1)/2-2=(3x-2)/10-(2x+3)/5
去分母(方程两边同乘各分母的最小公倍数)得,
↓
5(3x+1)-10×2=(3x-2)-2(2x+3)
去括号得,
↓
15x+5-20=3x-2-4x-6
移项得,
↓
15x-3x+4x=-2-6-5+20
合并同类项得,
↓
16x=7
系数化为1得,
↓
x=7/16.
字母公式
a=b a+c=b+c a-c=b-c
a=b ac=bc
a=bc(c≠0)= a÷c=b÷c
求根公式
由于一元一次方程是基本方程,故教科书上的解法只有上述的方法.
但对于标准形式下的一元一次方程 aX+b=0
可得出求根公式 X= -(b/a)
 富港检测东莞有限公司
富港检测东莞有限公司
2024-12-25 广告
正弦振动多用于找出产品设计或包装设计的脆弱点。看在哪一个具体频率点响应最大(共振点);做正弦振动找富港,富港工业检测技术有限公司是一家专业的第三方检测机构,拥有完善的质量管理体系,先进的检测设备,优秀的技术人才;已取得CNAS、CMA、IS...
点击进入详情页
本回答由富港检测东莞有限公司提供
2022-01-04
展开全部
北师大版四年级数学下册有一个单元是方程,关于解方程的方法,课本上只讲了一种方法,就是利用等式性质解方程,用这种方法可以解决课本上的所有练习题,学生们对这种方法也能很好地掌握。但是用这种方法,学生却不知道怎么解练习册、测试卷子上的形如30÷2X=5的方程。
前几天我曾写过一篇关于一道方程形如8-3X=2的文章,图文结合,详细讲解了用两种方法解这个类型的方程。收藏和分享那篇文章的人很多,相信会对一些学生、家长有帮助。今天我再把教学中遇到的,学生出错率高的问题变成文字,希望能帮到更多的学生。
先回顾一下形如8-3X=2的方程的解法。
某学错误的解法如图1
图1
现在我把图中的方程作为例题,再回顾一下它的两种解法:
30-6X=6
第一种方法(利用等式性质):(解题过程见图2)
图2
第二种方法(根据四则运算的文字表达式):(解题过程见图3)
图3
下面现在开始说形如30÷2X=5的方程。先来看一下某位学生错误的解法(图4)
图4
图中这个方程,即使学生会方法,也仍然计算不出来,因为计算时要么用到小数除法,要么用到分数乘法,两者都已经严重超出了四年级学生的知识范围。
所以我以30÷2X=5为例,同样用上面的两种方法解这个方程。
第一种方法(根据等式性质):(见图5)
图5
第二种方法(根据四则运算的文字表达式):(见图6)
图6
一点说明:图3和图6中的“思路、依据”是脑子里面思考的过程,在实际解方程时不用写出来,只要自己明白就可以了。
从上面的解题过程不难发现,第二种方法是比较简单的,条件是:学生要熟记四则运算的十二种(主要是八种)文字表达式(或者说关系式)。而且这种方法,是以后继续深入学习解方程的最常用、最方便的方法。
不知道现在使用的这本教材的编写者出于什么原因,要使用等式性质解方程,看起来学生容易掌握,其实写的过程繁琐,而且到了高年级和初中、高中以后,几乎是不用这种方法解法程的。
所以,我建议学生,要熟练掌握第二种解方程的方法,为继续学习打好基础。
前几天我曾写过一篇关于一道方程形如8-3X=2的文章,图文结合,详细讲解了用两种方法解这个类型的方程。收藏和分享那篇文章的人很多,相信会对一些学生、家长有帮助。今天我再把教学中遇到的,学生出错率高的问题变成文字,希望能帮到更多的学生。
先回顾一下形如8-3X=2的方程的解法。
某学错误的解法如图1
图1
现在我把图中的方程作为例题,再回顾一下它的两种解法:
30-6X=6
第一种方法(利用等式性质):(解题过程见图2)
图2
第二种方法(根据四则运算的文字表达式):(解题过程见图3)
图3
下面现在开始说形如30÷2X=5的方程。先来看一下某位学生错误的解法(图4)
图4
图中这个方程,即使学生会方法,也仍然计算不出来,因为计算时要么用到小数除法,要么用到分数乘法,两者都已经严重超出了四年级学生的知识范围。
所以我以30÷2X=5为例,同样用上面的两种方法解这个方程。
第一种方法(根据等式性质):(见图5)
图5
第二种方法(根据四则运算的文字表达式):(见图6)
图6
一点说明:图3和图6中的“思路、依据”是脑子里面思考的过程,在实际解方程时不用写出来,只要自己明白就可以了。
从上面的解题过程不难发现,第二种方法是比较简单的,条件是:学生要熟记四则运算的十二种(主要是八种)文字表达式(或者说关系式)。而且这种方法,是以后继续深入学习解方程的最常用、最方便的方法。
不知道现在使用的这本教材的编写者出于什么原因,要使用等式性质解方程,看起来学生容易掌握,其实写的过程繁琐,而且到了高年级和初中、高中以后,几乎是不用这种方法解法程的。
所以,我建议学生,要熟练掌握第二种解方程的方法,为继续学习打好基础。
本回答被网友采纳
已赞过
已踩过<
评论
收起
你对这个回答的评价是?
展开全部
这是一个不定方程,没有固定的解。也有可能题抄错了。
这种方程使用加减消元,或者代入消元都可以。
以加减法为例:
∠1+∠2=114…………………………(1)
∠3+∠4=78…………………………(2)
∠1+∠3=42……………………………(3)
∠2+∠4=150…………………………(4)
1、分析:
方程(1)-方程(3)消去∠1,得:
∠2-∠3=72……………………………(5)
方程(4)-方程(2)消去∠4,得:
∠2-∠3=72……………………………(6)
与方程5是同解方程,因此该方程组有无数组解,属于不定方程。
请再去认真检查原题抄写是否有误。
2、换一种思路:
方程(1)+方程(2),得:
∠1+∠2+∠3+∠4=192………………(7)
方程(7)-方程(3),得:
∠2+∠4=150
与方程(4)完全相同,也就是说,方程(4)相对于方程(1)、(2)、(3)来说,并没有给出新的数量关系。方程(4)的等量关系隐含在方程(1)、(2)、(3)中,相当于四个未知数,只给出三个方程的方程组。一般情况下有无穷多组解。
这种方程使用加减消元,或者代入消元都可以。
以加减法为例:
∠1+∠2=114…………………………(1)
∠3+∠4=78…………………………(2)
∠1+∠3=42……………………………(3)
∠2+∠4=150…………………………(4)
1、分析:
方程(1)-方程(3)消去∠1,得:
∠2-∠3=72……………………………(5)
方程(4)-方程(2)消去∠4,得:
∠2-∠3=72……………………………(6)
与方程5是同解方程,因此该方程组有无数组解,属于不定方程。
请再去认真检查原题抄写是否有误。
2、换一种思路:
方程(1)+方程(2),得:
∠1+∠2+∠3+∠4=192………………(7)
方程(7)-方程(3),得:
∠2+∠4=150
与方程(4)完全相同,也就是说,方程(4)相对于方程(1)、(2)、(3)来说,并没有给出新的数量关系。方程(4)的等量关系隐含在方程(1)、(2)、(3)中,相当于四个未知数,只给出三个方程的方程组。一般情况下有无穷多组解。
已赞过
已踩过<
评论
收起
你对这个回答的评价是?
更多回答(1)
推荐律师服务:
若未解决您的问题,请您详细描述您的问题,通过百度律临进行免费专业咨询