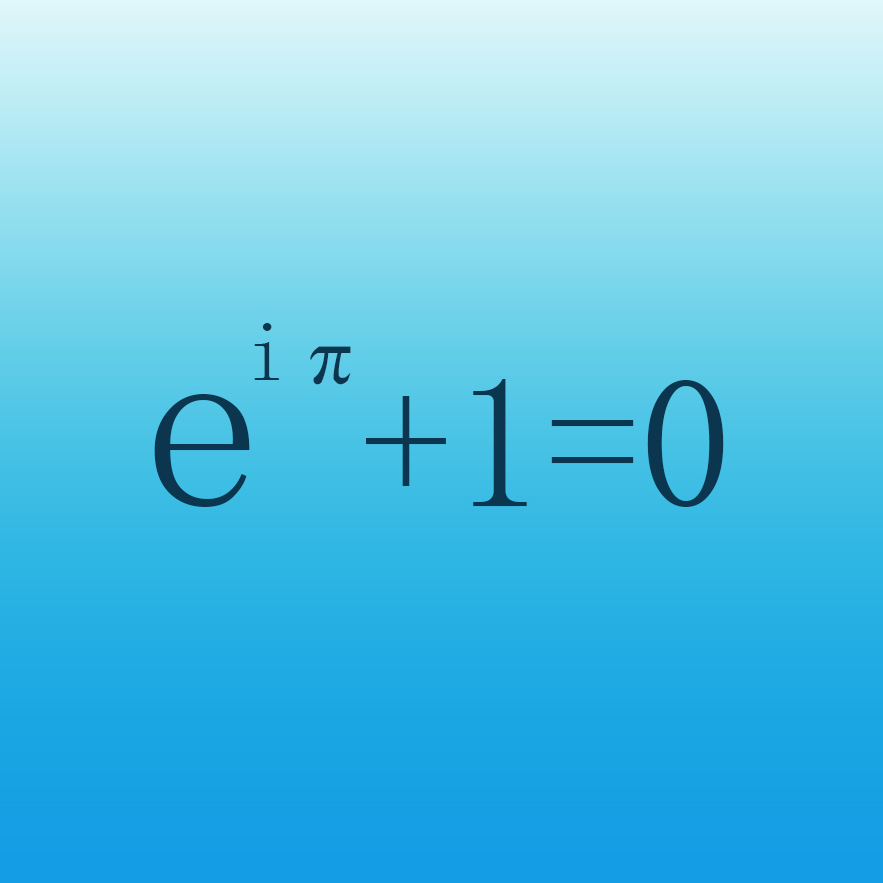еҫҲеӨҡеӯҰз”ҹ他们зҡ„дёүи§’еҮҪж•°еӯҰеҫ—еҫҲе·®пјҢжңүд»Җд№ҲиЎҘж•‘ж–№жі•пјҹ
2021-02-09 В· ж•ҷиӮІйўҶеҹҹеҲӣдҪңиҖ…

еҮҪж•°еҜ№еҫҲеӨҡеҲқй«ҳдёӯз”ҹжқҘиҜҙйғҪжҳҜдёҖдёӘйҡҫзӮ№пјҢдҪҶжҳҜеӣ дёәеҮҪж•°жҳҜеҲқй«ҳдёӯж•°еӯҰзҡ„йҮҚзӮ№зҡ„зјҳж•…пјҢеҜјиҮҙдёҚз®ЎеңЁеҲқдёӯиҝҳжҳҜеңЁй«ҳдёӯж¶үеҸҠеҲ°зҡ„зҹҘиҜҶзӮ№е’ҢиҖғзӮ№йғҪйқһеёёзҡ„еӨҡгҖӮ
жҜ”еҰӮй«ҳдёӯж•°еӯҰзҡ„дёүи§’еҮҪж•°пјҢеӣ дёәе…¶е…¬ејҸеӨҡпјҢеӣҫеғҸеӨҡпјҢжҖ§иҙЁеӨҡпјҢеҜјиҮҙиҖғзӮ№еӨҡпјҢиҖҢдё”жҳҜжҜҸе№ҙй«ҳиҖғж•°еӯҰдёӯеҲҶж•°еҚ жҜ”жңҖеӨ§зҡ„иҖғзӮ№д№ӢдёҖпјҢжӯӨеӨ–еӯҰеҘҪдёүи§’еҮҪж•°иҝҳиғҪеңЁеҫҲеӨ§зЁӢеәҰдёҠеё®еҠ©еҗҢеӯҰ们еӯҰд№ жҺҢжҸЎзү©зҗҶйҮҚйҡҫзӮ№дёӯзҡ„еј№з°§жҢҜеӯҗгҖҒжіўзӯүзӣёе…ізҹҘиҜҶгҖӮ
зӣёдҝЎжңүеҫҲеӨҡй«ҳдёӯз”ҹзҡ„дёүи§’еҮҪж•°еӯҰзҡ„йғҪдёҚеӨӘеҘҪпјҢеңЁ2020е№ҙдәәж•ҷзүҲеҝ…дҝ®дёҖзҡ„ж”№зүҲж–°ж•ҷжқҗдёӯпјҢдёүи§’еҮҪж•°жңҖејҖе§ӢеҮәзҺ°еңЁгҖҠ第дә”з« дёүи§’еҮҪж•°гҖӢгҖӮдёӢйқўз»ҷеҮәдёӨдёӘжңҖе…ій”®зҡ„ж–№жі•е’Ңе»әи®®пјҡзҹҘиҜҶжЁЎеқ—зҡ„зі»з»ҹеҢ–еӯҰд№ е’ҢиҮӘиә«зҡ„дё»еҠЁеӯҰд№ гҖӮ
第дёҖпјҢзі»з»ҹеҢ–еӯҰд№ гҖӮ
зі»з»ҹеҢ–еӯҰд№ пјҢиҝҷе°ұжҳҜиҜҙжҲ‘们дёҚиғҪвҖңзјәе•ҘиЎҘе•ҘвҖқгҖӮдёҚиғҪеӣ дёәдёүи§’еҮҪж•°зҡ„еӣҫеғҸгҖҒиҜұеҜје…¬ејҸзӯүжІЎеӯҰеҘҪе°ұеҸӘиЎҘд№ дёүи§’еҮҪж•°зҡ„еӣҫеғҸе’ҢиҜұеҜје…¬ејҸйғЁеҲҶгҖӮйӮЈж ·еҒҡзҡ„иҜқпјҢдёҖж–№йқўжҳҜиЎҘд№ зҡ„ж•ҲжһңдёҚеӨӘеҘҪпјҢеҸҰдёҖж–№йқўдёҚеҲ©дәҺзҹҘиҜҶзҡ„зҶҹз»ғжҺҢжҸЎе’Ңж·ұеҲ»зҗҶи§ЈгҖӮ
д№ҹе°ұжҳҜиҜҙжҲ‘们иҰҒд»ҺиҜҫжң¬дёҠгҖҠ第дә”з« дёүи§’еҮҪж•°гҖӢзҡ„第дёҖиҠӮгҖҠд»»ж„Ҹи§’е’Ңеј§еәҰеҲ¶гҖӢејҖе§Ӣи®ӨзңҹеӨҚд№ гҖҒд»”з»ҶзҗҶи§ЈгҖӮиҝҷж ·иө°дёӢжқҘжңүеҠ©дәҺзҹҘиҜҶзҡ„зі»з»ҹеҢ–пјҢиҖҢдё”жӣҙе®№жҳ“ж°ҙеҲ°жё жҲҗзҡ„зҗҶи§ЈдёӢдёҖиҠӮгҖҠдёүи§’еҮҪж•°зҡ„жҰӮеҝөгҖӢ е’ҢгҖҠиҜұеҜје…¬ејҸгҖӢзӯүеҶ…е®№гҖӮ
зі»з»ҹеҢ–еӯҰд№ зҡ„еҘҪеӨ„жҳҜпјҢдёҚдҪҶиғҪеё®еҠ©еҗҢеӯҰ们жҢүж–°й«ҳиҖғиҜҫзЁӢж ҮеҮҶиҰҒжұӮзҡ„йӮЈж ·д»Һж №жң¬дёҠзҗҶи§ЈеҲ°дҪҚпјҢиҝҳиғҪеё®еҠ©еҗҢеӯҰ们еҝ«йҖҹгҖҒзҶҹз»ғең°жҺҢжҸЎдёүи§’еҮҪж•°зҡ„зӣёе…ізҹҘиҜҶе’Ңи§Јйўҳж–№жі•жҠҖе·§гҖӮ
第дәҢпјҢиҮӘиә«зҡ„дё»еҠЁеӯҰд№ гҖӮ
иҜҙеҲ°дёүи§’еҮҪж•°зҡ„жҰӮеҝөпјҢжҲ‘们иҰҒз»“еҗҲе®ҡд№үзҗҶи§ЈеҲ°жҠҠд»»ж„ҸдёҖдёӘи§’ж”ҫеҲ°еқҗж Үзі»дёӯпјҢи®©и§’зҡ„иө·е§Ӣиҫ№дёҺxиҪҙзҡ„йқһиҙҹеҚҠиҪҙпјҲеқҗж Үзі»еҺҹзӮ№е’ҢxиҪҙзҡ„жӯЈеҚҠиҪҙпјүйҮҚеҗҲпјҢи§ЈеҮәи§’зҡ„з»Ҳиҫ№дёҺеңҶеҝғеңЁеҺҹзӮ№зҡ„еҚ•дҪҚеңҶдәӨзӮ№зҡ„еқҗж ҮпјҢи®ҫдёәпјҲx,yпјүзҡ„иҜқпјҢйӮЈд№ҲиҝҷдёӘи§’зҡ„жӯЈејҰеҖје°ұзӯүдәҺxпјҢиҝҷдёӘи§’зҡ„дҪҷејҰеҖје°ұзӯүдәҺyпјҢиҝҷдёӘи§’зҡ„жӯЈеҲҮеҖје°ұзӯүдәҺy/xгҖӮ
жүҖд»ҘпјҢеңЁдёҠйқўдёүи§’еҮҪж•°зҡ„жҰӮеҝөдёӯпјҢжҲ‘们дёҚйҡҫжҖ»з»“еҮәпјҢжұӮд»»ж„ҸдёҖдёӘи§’зҡ„дёүдёӘдёүи§’еҮҪж•°еҖјпјҢе…¶е®һе°ұеҸӘиҰҒжұӮеҮәиҝҷдёӘи§’дёҺеҚ•дҪҚеңҶдәӨзӮ№зҡ„еқҗж ҮпјҲx,yпјүпјҢ然еҗҺеҫҖзӣёеә”зҡ„дёүи§’еҮҪж•°еҖјзҡ„е®ҡд№үдёӯд»ЈеҚіеҸҜгҖӮ
еӯҰе®Ңдёүи§’еҮҪж•°зҡ„жҰӮеҝөеҗҺпјҢдёҚиҰҒжҖҘзқҖеҫҖдёӢйў„д№ гҖӮжҲ‘们дёҚеҰЁеҶҚеҜ№дёүи§’еҮҪж•°зҡ„жҰӮеҝөиҝҷйғЁеҲҶзҹҘиҜҶиҝӣиЎҢиҝӣдёҖжӯҘзҡ„зҗҶи§Је’ҢжҺўз©¶гҖӮз”ЁиҮӘе·ұеҜ№дёүи§’еҮҪж•°жҰӮеҝөзҡ„зҗҶи§ЈпјҢжқҘжҺўз©¶е’ҢеҸ‘зҺ°дёүи§’еҮҪж•°жҰӮеҝөдёӯи•ҙи—Ҹзҡ„жӣҙеӨҡзҹҘиҜҶгҖӮ
жҜ”еҰӮпјҢз”ұеҚ•дҪҚеңҶзҡ„еҚҠеҫ„дёә1пјҢеңҶеҝғеңЁеҺҹзӮ№пјҢеҫ—еҲ°xеӨ§дәҺзӯүдәҺ-1пјҢдё”е°ҸдәҺзӯүдәҺ-1гҖӮз»“еҗҲxеҖјеҚідёәи§’зҡ„дҪҷејҰеҖјпјҢеҸҜеҫ—д»»ж„Ҹи§’зҡ„дҪҷејҰеҖјзҡ„еҖјеҹҹдёәеӨ§дәҺзӯүдәҺ-1пјҢдё”е°ҸдәҺзӯүдәҺ1гҖӮ
д»ҘжӯӨзұ»жҺЁпјҢдёҚйҡҫеҫ—еҲ°жӯЈејҰеҮҪж•°зҡ„еҖјеҹҹгҖҒжӯЈеҲҮеҮҪж•°зҡ„еҖјеҹҹпјҢд»ҘеҸҠе®ғ们зҡ„жңҖеӨ§еҖјгҖҒжңҖе°ҸеҖјпјҢи§’еҲҶеҲ«еҸ–еҖјж—¶еҜ№еә”зҡ„дёүи§’еҮҪж•°еҖјеҸ–жңҖеҖјпјҢеҸҠи§’зҡ„з»Ҳиҫ№еңЁеҗ„дёӘиұЎйҷҗж—¶дёүи§’еҮҪж•°еҖјзҡ„жӯЈиҙҹй—®йўҳгҖӮ
еҶҚеҰӮпјҢжҲ‘们еҸҜд»Ҙж №жҚ®и§’з»Ҳиҫ№ж—ӢиҪ¬зҡ„е‘ЁжңҹжҖ§еҫ—еҲ°жӯЈејҰеҮҪж•°гҖҒдҪҷејҰеҮҪж•°зҡ„е‘ЁжңҹгҖӮд№ҹиғҪеҸ‘зҺ°з»Ҳиҫ№зӣёеҗҢзҡ„и§’дёҺеҚ•дҪҚеңҶзҡ„дәӨзӮ№еқҗж ҮзӣёеҗҢгҖӮйӮЈд№Ҳж №жҚ®дёүи§’еҮҪж•°зҡ„жҰӮеҝөпјҢз»Ҳиҫ№зӣёеҗҢзҡ„и§’зҡ„дёүдёӘдёүи§’еҮҪж•°еҖјеҜ№еә”зӣёзӯүгҖӮжңүжӯӨжғіжі•еҗҺжҲ‘们е°ұиҮӘдё»е®ҢжҲҗжң¬иҠӮвҖңиҜұеҜје…¬ејҸдёҖвҖқзҡ„зҗҶи§Је’ҢжҺЁеҜјгҖӮ
йҖҡиҝҮжҲ‘们иҮӘдё»жҺўз©¶жқҘз ”з©¶й—®йўҳзҡ„иғҪеҠӣпјҢжҳҜж–°й«ҳиҖғж”№йқ©иҰҒжұӮе…·еӨҮзҡ„дёҖдёӘе…ій”®иғҪеҠӣд№ӢдёҖгҖӮжҲ‘们йҖҡиҝҮиҮӘдё»жҺўз©¶жҺЁеҜјпјҢж— еҪўдёӯе°ұеҹ№е…»иө·дәҶиҮӘе·ұзҡ„иҝҷж–№йқўиғҪеҠӣгҖӮеҸҰеӨ–пјҢеҶҚзҝ»зңӢиҜҫжң¬еҗҺеҸ‘зҺ°з»“и®әеұ…然е’ҢиҮӘе·ұжҺЁеҜјзҡ„з»“жһңдёҖж ·пјҢеңЁеӯҰд№ дёҠзҡ„жҲҗеҠҹж„ҹгҖҒиҮӘдҝЎж„ҹе’ҢеҜ№ж•°еӯҰзҡ„еӯҰд№ е…ҙи¶ЈеҫҲиҮӘ然зҡ„е°ұжҝҖеҸ‘дәҶеҮәжқҘгҖӮ
иҝҷе°ұжҳҜдё»еҠЁеӯҰд№ зҡ„еҘҪеӨ„гҖӮеҗҢеӯҰ们дёҖж—ҰжңүдәҶиҝҷз§ҚиҮӘдё»еӯҰд№ дә§з”ҹзҡ„еӯҰд№ д№җи¶ЈеҗҺпјҢйӮЈд№Ҳд»ҘеҗҺиҮӘдё»еӯҰд№ зҡ„ж¬Іжңӣе’ҢеҠЁеҠӣе°ұиҮӘ然иҖҢ然ең°иў«жҝҖеҸ‘дәҶеҮәжқҘгҖӮ
еҗҺз»ӯзҡ„еҶ…е®№гҖҠиҜұеҜје…¬ејҸгҖӢгҖҒгҖҠдёүи§’еҮҪж•°зҡ„еӣҫеғҸдёҺжҖ§иҙЁгҖӢгҖҒгҖҠдёүи§’жҒ’зӯүеҸҳжҚўгҖӢзӯүпјҢд№ҹиҰҒйҮҚи§Ҷиө·зҹҘиҜҶжЁЎеқ—зҡ„зі»з»ҹеҢ–еӯҰд№ е’Ңдё»еҠЁеӯҰд№ гҖӮиҝҷж ·еӯҰд№ дёӢжқҘеҗҺпјҢеӨҙи„‘дёӯдёҚдҪҶдјҡеҜ№иҝҷз« зҹҘиҜҶзҡ„и„үз»ңзү№еҲ«жё…жҘҡпјҢиҖҢдё”д№ҹдјҡеҜ№иҝҷйғЁеҲҶзҡ„зҹҘиҜҶйғҪдәҶеҰӮжҢҮжҺҢгҖӮдёүи§’еҮҪж•°иҝҷз« йҮҢзҡ„еҫҲеӨҡе…¬ејҸе’ҢзҹҘиҜҶзӮ№зӯүдёҚеҝ…еҲ»ж„ҸиҠұеӨ§йҮҸж—¶й—ҙи®°еҝҶпјҢе°ұе·Із»ҸиҮӘ然иҖҢ然ең°жҺҢжҸЎйҖҸдәҶгҖӮ
еӯҰйңёд№ӢжүҖд»ҘдёәеӯҰйңёжӯЈжҳҜеӣ дёә他们йғҪжҳҜеңЁдё»еҠЁеӯҰд№ пјҢд»ҺдёҚе–ңж¬ўиў«еҠЁеӯҰд№ гҖӮиҖҢеҸӘжңүжҲ‘们иҮӘе·ұеҺ»дё»еҠЁеӯҰд№ пјҢиҮӘиә«йҡҗи—Ҹзҡ„е·ЁеӨ§жҪңеҠӣжүҚиғҪиў«жҝҖеҸ‘еҮәжқҘгҖӮиў«еҠЁеӯҰд№ зҡ„з»“жһңжҳҜвҖңеӯҰе•Ҙе•ҘдёҚдјҡвҖқзҡ„иҜқпјҢ дё»еҠЁеӯҰд№ зҡ„з»“жһңе°ұдёәвҖңеӯҰе•Ҙе•ҘиғҪжҲҗвҖқгҖӮ
2021-02-10 В· еҸӨд»ҠеӨҡе°‘дәӢгҖҒйғҪд»ҳ笑и°ҲдёӯпјҒ

2021-02-10